题目： 812.最大三角形面积

题面

给你一个由 X-Y 平面上的点组成的数组 points ，其中 points[i] = [x<sub>i</sub>, y<sub>i</sub>] 。从其中取任意三个不同的点组成三角形，返回能组成的最大三角形的面积。与真实值误差在 10<sup>-5</sup> 内的答案将会视为正确答案。

示例

示例 1：

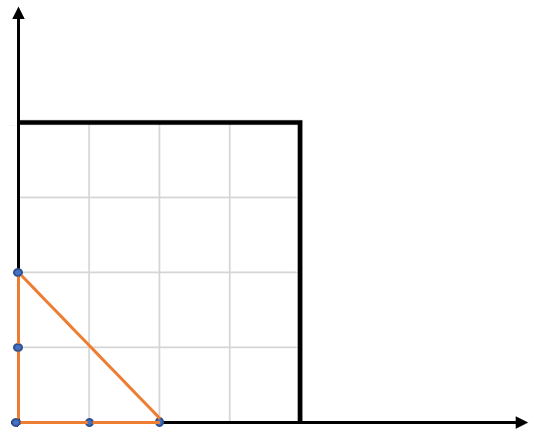
输入：points = [[0,0],[0,1],[1,0],[0,2],[2,0]]
输出：2.00000
解释：输入中的 5 个点如上图所示，红色的三角形面积最大。

示例 2：

输入：points = [[1,0],[0,0],[0,1]]
输出：0.50000

Tips

  • 3 <= points.length <= 50
  • -50 <= x<sub>i</sub>, y<sub>i</sub> <= 50
  • 给出的所有点 互不相同

Code

代码解释

这段 C++ 代码的目的是在给定的一组二维平面上的点中，找到面积最大的三角形，并返回该面积。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
    double largestTriangleArea(vector<vector<int>>& points) {
        int n = points.size();  // 获取点的数量
        double res = 0;  // 初始化最大面积为0
    
        // 三重循环遍历所有不同的点组合
        for(int i = 0; i < n; ++i) {
            for(int j = 0; j < i; ++j) {
                for(int k = 0; k < j; ++k) {
                    // 获取三个点的坐标
                    int x1 = points[i][0], y1 = points[i][1];
                    int x2 = points[j][0], y2 = points[j][1];
                    int x3 = points[k][0], y3 = points[k][1];
                
                    // 计算三条边的长度
                    double a = sqrt(pow(x1 - x2, 2) + pow(y1 - y2, 2));
                    double b = sqrt(pow(x2 - x3, 2) + pow(y2 - y3, 2));
                    double c = sqrt(pow(x1 - x3, 2) + pow(y1 - y3, 2));
                
                    // 使用海伦公式计算三角形面积
                    double p = (a + b + c) / 2;  // 计算半周长
                    double s = sqrt(p * (p - a) * (p - b) * (p - c));  // 计算面积
                
                    // 更新最大面积
                    res = max(res, s);
                }
            }
        }
    
        return res;  // 返回最大面积
    }
};

逐行解释

  1. int n = points.size();:

    • 获取输入的点的数量，并存储在变量 n 中。

  2. double res = 0;:

    • 初始化变量 res，用于存储最大三角形面积。初始值为0。

  3. for(int i = 0; i < n; ++i) { ... }:

    • 使用三重嵌套循环，枚举所有可能的点组合。这三个循环确保从 points 中选择三个不同的点，构成一个三角形。

  4. int x1 = points[i][0], y1 = points[i][1];:

    • 这三行分别从 points 数组中提取当前选中的三个点的坐标 (x1, y1)、(x2, y2) 和 (x3, y3)。

  5. double a = sqrt(pow(x1 - x2, 2) + pow(y1 - y2, 2));:

    • 计算两点之间的距离，使用的是欧几里得距离公式。a、b、c 分别表示三角形的三条边。

  6. double p = (a + b + c) / 2;:

    • 计算三角形的半周长 p，即三条边之和除以2。

  7. double s = sqrt(p * (p - a) * (p - b) * (p - c));:

    • 使用海伦公式计算三角形的面积 s。海伦公式根据三条边的长度计算三角形面积。

  8. res = max(res, s);:

    • 通过比较当前计算的三角形面积 s 与之前的最大面积 res，更新 res，保留最大的三角形面积。

  9. return res;:

    • 返回最大三角形的面积。

逻辑总结

  • 该代码的核心思想是通过枚举所有可能的三角形组合，使用海伦公式计算每个三角形的面积，并最终找到并返回最大的三角形面积。
  • 时间复杂度为 O(n^3)，因为它通过三重循环遍历所有可能的点组合。在点数较少时，这是可行的，但如果点数很多，算法的效率会受到限制。

假设 points 数组中有 4 个点 [ [0,0], [0,1], [1,0], [1,1] ]：

  1. 枚举出所有三角形组合。
  2. 计算每个三角形的面积。
  3. 找到面积最大的那个三角形，并返回其面积。